An interesting time has come in my life. After spending 6 years in Szczecin I’ve decided that I needed change. I quit my job, moved out from Szczecin and currently am currently pursuing a life that’s more aligned with my values. During last six years I’ve learned a lot in general and much about myself as well. I saw a tension growing between curiosity and security. I’ve discovered that I drifted too much from my initial intrest in economics towards practical problem solving using data analysis and programming. Adding to that my dwindling attachment to security, growing tolerance of calculated risk taking and unfulfilled urge for growth I decided to steer my life differently.
I’ve given myself two month of space in my life form the demands of work. I remembered once getting inspired by a story told me during a conference of a bike trip around the Baltic Coast. I just felt that I wanted to do something similar. I’ve discovered the whole Eurovelo network of international European cycling routes. Of course couple of months on the road sounded more like an escape from life, than just taking some space to rethink my values and future direction. I’ve decided to go for a month long bike journey around Sweden, Finland and Estonia. I decided to go for an adventure!
In short:
I developed a small Python script that allows me to download and prepare for print OSM tiles along a track from GPX files. It enables me to download tiles, stitch them together, add a scale and process them for multi-page printing using selected by me scale. It serves great help for creating printed maps for hiking/biking/tourism from OSM and other tile server sites.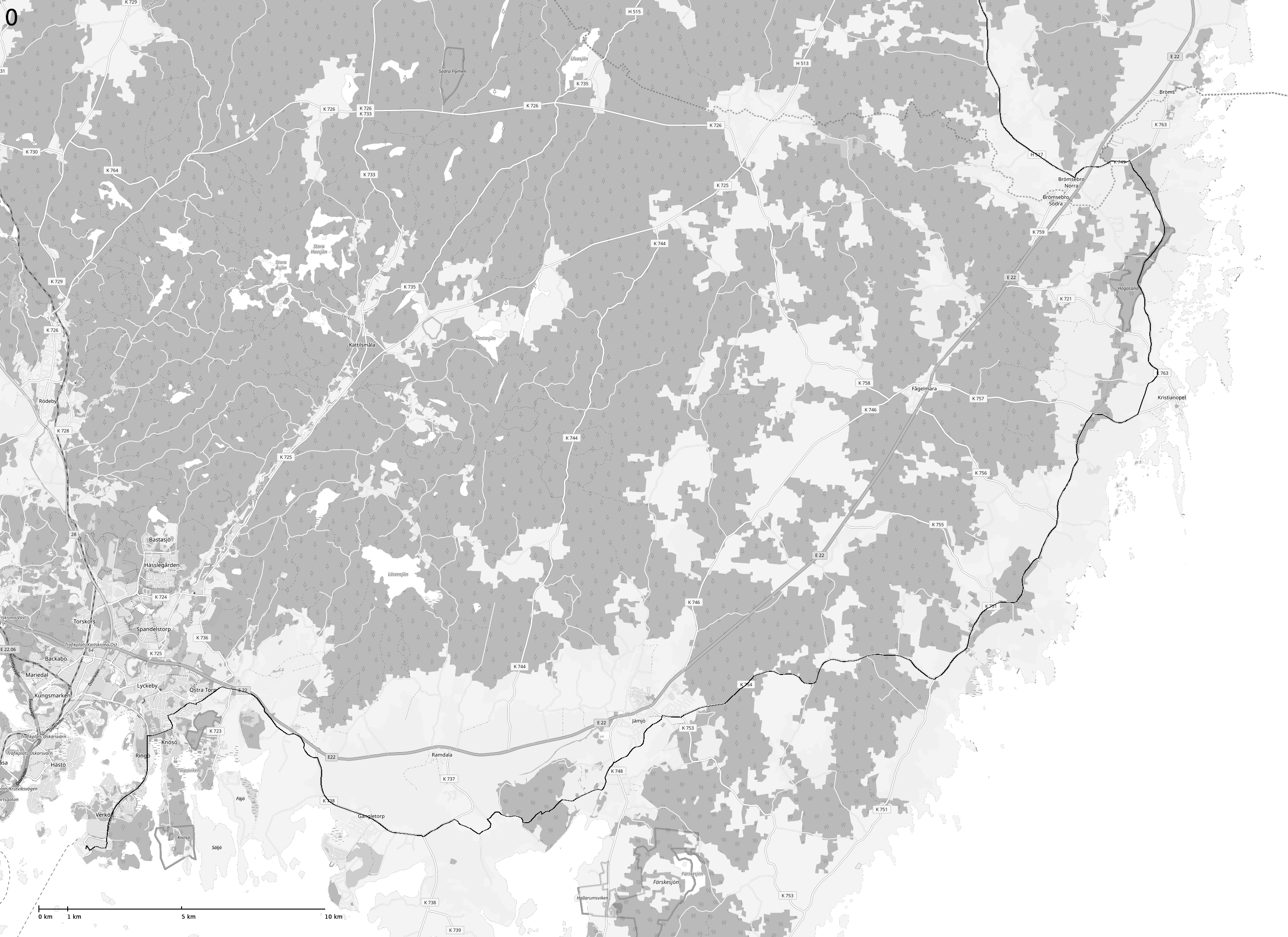 
. The code is freely avaliable as a GitHub repository.
Planing
The typical pre-travel arrangements included route planning. In the past I’ve been using the GPSies website for planning. It proved useful for generating tracks alongside roads. I just remembered that it was hard to modify an already existing track. I remembered that after creating a track the website stored the results as points along the way. Even when it was easy to create a track just by selecting couple of points, and the website calculated all the rest, sticking new points to the most optimal track, it was difficult to change an already existing one. I had to change everything manually point by point or start anew.
I found BikeMap to be a much better solution for route design. It calculated my route automatically given start and end points and allowed for flexible adjustments by dragging selected points and snapping them to best routes. It also could show bike routes as well. It allows to save routes for further modifications that do not require to drag every point separately but employ the same snap-to-route approach. The only disadvantage is its success. The site can be slow at times even to the point of non-responsiveness.
For quick cycle route design I use cycle travel. It has all the advantages of the former, but without its slow speed. It’s the fastest of the selected three. It also provides the same snap functionality for route modification. What I found a bit daunting is that it shows all the directions in the left pane, which in case of an over 1500 km route creates chaos instead of providing information.
All of the three sites can export GPX routes as well as save them online. My initial design was using Bike Map site. The whole route is publically avaliable.
Printing maps
Obtaining OSM tiles
Having planned my route and obtaining it in a GPX format I needed a map. I will have my phone with offline OSMAnd maps, but I still would rather relay on paper maps. Having electronic GPS is convenient, but I find it risky. A phone without power could easily jeopardize the whole trip and that’s a risk I’m not willing to take. I had this idea of printing OpenStreetMaps data on paper.
Of course I wasn’t the first person with this idea. Actually there’s a whole OSM on Paper page dedicated listing all the software that could be used to printing such maps. I tried some of the dedicated on-line websites. They were either not flexible enough for my needs or did not allow for enough control of the results allowing only creation of low-zoom maps.
I checked out GMapCatcher. It’s a program written in Python 2.7 and introduces a nice GTK GUI to interact with the maps. It provides the functionality to download tiles only around a predefined GPX track. After the first run buy default it creates a folder in the user’s home directory where it keeps all the settings and downloaded maps.
The program operates using non-standard zoom values, so it’s best to check the zoom level before downloading the tiles. The programs provides a non-GUI command to download tiles along the GPX track. An example call is shown below.
python2 download.py --gpx=~/gis/sweden_trip/cycle_travel.gpx --min-zoom=5 --max-zoom=5 --width=5
There are around 4000 tiles at this zoom level, so it takes a bit of time to complete. By default it downloads tiles from the server selected in the GUI in Settings / Change Theme / Map service.
After the download completes we can open the GUI and see the new tiles being avaliable offline. When we want to download additional, missing tiles we can just uncheck the Offline box in the main window and the software should download the tiles on the fly.
After downloading the tiles need to be exported into OSM folder structure {zoom}/{lon}/{lat}.png using the Operations / Map tiles export from the main menu.
Stitching tiles together
Having obtained tiles along my future travel path I decided to stitch the together into printable images. I started a Python project where at first I just wanted to divide tiles and stitch them together. But, as it usually is I ended up creating a tool more universal than I expected.
OSM tiles are generated in 256 x 256 px PNG images. For each zoom level a subfolder is created and in each such zoom subfolder a subfolder for each column is created containing PNG files for each row of this column (more info).
Imagining Earth on a Longitude x Latitude (X x Y) plane we can interpret the zoom level as dividing each of two dimmensions into $2^{2 \times zoom}$ equal squares. Thus for example for the zoom level 13, we get 67 108 864 tiles. OSM Wiki provides Python code to obtain tile X and Y cooordinates from lon and lat geographical coordinates and other way around.
Using simple Python code I can walk the zoom subdirectory and create a set of (X, Y) tiles available offline. I decided to use a set of tuples, because no (X, Y) tuple can be present more than once and the order of tuples does not matter for me. I used a combination of os.walk() and regular expressions to generate existing lon and lat.
def get_tiles(path):
"""Read avaliable tiles into a set"""
tiles = set({})
for files in os.walk(path):
if len(files[2]) == 0:
continue
x = re.search(r'/([0-9]+)$', files[0])[1]
for f in files[2]:
y = re.search('[0-9]+', f)[0]
tiles.add((int(x), int(y)))
print("Found %s tiles." % len(tiles))
return tiles
Based on that I calculated the range of avaliable tiles and saved it as a tile_range dictionary.
x = [xy[0] for xy in tiles]
y = [xy[1] for xy in tiles]
tile_range = {
'x': [min(x), max(x)],
'y': [min(y), max(y)],
'dx': max(x) - min(x),
'dy': max(y) - min(y)
}
I used this information to construct a NumPy boolean array with 1 indicating where the tiles were present:
tile_array = np.zeros((tile_range['y'][1] - tile_range['y'][0] + 1, tile_range['x'][1] - tile_range['x'][0] + 1))
for c in tiles:
tile_array[c[1] - tile_range['y'][0], c[0] - tile_range['x'][0]] = 1
I then used matplotlib pyplot.matshow() to save my canvas:
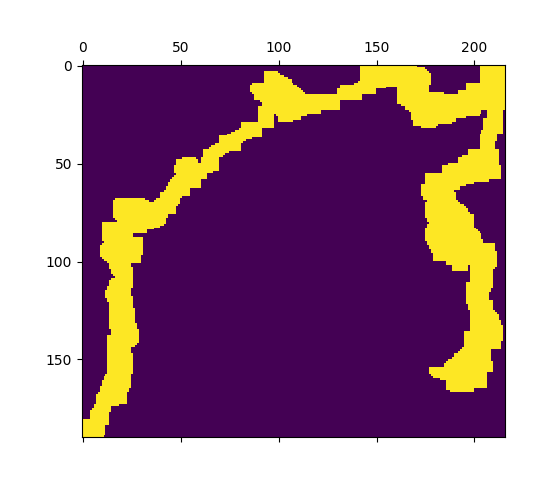
Besides creating a Tiles class to hold my tiles I also created a Box class to define boxes which I will be using to cut tiles from my set of tiles avaliable offline. It’s a simple object with x, y, dx, dy properties, where x and y indicate the top corner coordinates (in the tile coordinate system) and dx and dy mean width and hight. I also calculate the bottom right corner in x1, y1. I also many more methods during development, from which I will only go into detail for couple of them.
The function responsible for drawing maps for prints is Box.stitch_array(). Based on the Box’s upper left and lower right coordinates it creates a set of tile coordinates tuples. It next uses a simple set difference to obtain missing tiles set based on the Tiles object’s .tiles property with avaliable offline image coordinates.
range_x = range(int(self.x), int(self.x1))
range_y = range(int(self.y), int(self.y1))
box_tiles = set([(x, y) for x in range_x for y in range_y])
missing_tiles = box_tiles - tiles.tiles
I next use PILlow’s Image.new() function to create an empty white canvas. I calculated the canvas’ size as the product of number of tile PNG image pixels per image and box’s width and height. I next loop over the set of box tile tuples and check if the current tile if not missing. If that is the case I load the tile using PIL’s Image.open(). In the end I paste current tile to the created before canvas.
# Create an empty image
result = Image.new('RGB', (x_size, y_size), color=(255, 255, 255))
# Read tiles if present and paste into canvas
for tile in box_tiles:
if tile in missing_tiles:
continue
tile_file = os.path.join(tiles.path, str(tiles.zoom), str(tile[0]), str(tile[1]) + '.png')
tile_image = Image.open(tile_file)
result.paste(im=tile_image, box=((tile[0]-self.x) * px_size[0], (tile[1]-self.y) * px_size[1]))
The function returns stitched tiles as PIL’s image, that needs to be saved later. At current stage Box coordinates work as integers. In the future I would like them to work as float numbers as well. I started to implement this, but I haven’t finished it yet, so I won’t go into details on this.
Creating Boxes around GPX track
At first I created a simple command dividing the whole tile array into rectangles of given width and height and then saving the stitched images whenever there was a tile present in the rectangle. Overall this algorithm was simple, but inefficient. It generated too many charts. Moreover the charts did not have the track on it and often the part where the actual track went was positioned suboptimally.
To add the track to the map I used Python gpxpy module. It loads the GPX file and produces list of tracks, segments and points. At this moment I assume that all the points are part of the same track and segment. For each point written in geographical coordinates I use the mentioned before procedure to convert them into OSM tile coordinates. Before adding them to the list of coordinates I check if the difference in any dimmention is less than 1. If it is not, I add middle points.
def add_middle_points():
"""Add middle points for sections skipping tiles"""
dx = x - lon[-1]
dy = y - lat[-1]
if abs(dx) >= 1 or abs(dy) >= 1:
nx = int(abs(dx))
ny = int(abs(dy))
n = max(nx, ny)
for _ in range(n):
lon.append(lon[-1] + dx / (n+1))
lat.append(lat[-1] + dy / (n+1))
lat = []
lon = []
gpx_track = gpxpy.parse(open(gpx, 'r'))
for track in gpx_track.tracks:
for segment in track.segments:
for point in segment.points:
x, y = utils.deg2num(point.latitude, point.longitude, zoom=self.zoom)
# Add middle points in case abs diff >= 1
if len(lat) > 1:
add_middle_points()
lon.append(x)
lat.append(y)
Having loaded my track I next generate Boxes around it using gen_boxes_from_track() function. It takes the GPX track as the first positional argument. Next dx and dy options define the width and height of each box ine tiles. Finally border allows to define a border around the track for each fragment for each chart.
The function is relatively simple. At first I created an empty list boxes containting all the resulting boxes. I then loop over each pair of the coordinates from the GPX track. At every point I calculate the extent using the Range object that holds the extent and returns the new extent upon adding new points. Whenever the new point exceed the currently held extent a new extent is calculated and returned. If that is not the case, the old one is returned. Range.reset() aims to reset the extent object before initializing each new Box. Objects P and L contain boolean values whether the new extent is within boundaries of the Box’s initial dimensions less the border. These conditions are calculated both for the portrait and landscape orientation of the box.
The trick here is that whenever a point exceeds either of the two extents (neither P nor L are true), that means that the previous extent was the final extent of the chart boundary box. Also based whether the previous extent was portrait a new boundary box is created as such. I also added a trick to center box horizontally or vertically so that the track occupies most of the center of the map. Such box is then added to the boxes list and variables holding previous values are reset.
def gen_boxes_from_track(track, dx=10, dy=10, border=1):
""" Generate boxes from track."""
# Initialize Range with empty range
Range.reset()
number_points = len(track[0])
boxes = []
prev_P = False
prev_extent = {}
# Loop over each point of track
for idx, point in enumerate(zip(track[0], track[1])):
extent = Range.get_extent(point)
# TODO: Allow for float coords in boxes
P = (extent['dx'] <= (dx - border)) and (extent['dy'] <= (dy - border))
L = (extent['dx'] <= (dy - border)) and (extent['dy'] <= (dx - border))
# If neither Portrait nor Landscape view fits, create end the rectangle
# from the previous fitting view
if len(prev_extent) > 0 and (((P or L) == False) or idx == number_points - 1):
if prev_P:
rot_dx = dx
rot_dy = dy
x = prev_extent['x'][0] - (rot_dx - prev_extent['dx']) / 2
y = prev_extent['y'][0]
else:
rot_dx = dy
rot_dy = dx
x = prev_extent['x'][0]
y = prev_extent['y'][0] - (rot_dy - prev_extent['dy']) / 2
boxes.append(Box(int(x), int(y), rot_dx, rot_dy))
prev_P = False
prev_extent = {}
Range.reset()
continue
prev_extent = extent
prev_P = P
return boxes
I also added the boxes to the legend plot together with the track. I ended up generating 52 charts. When I tried the division approach I ended up with over 90. The final result with boxes around the track looks something like this:
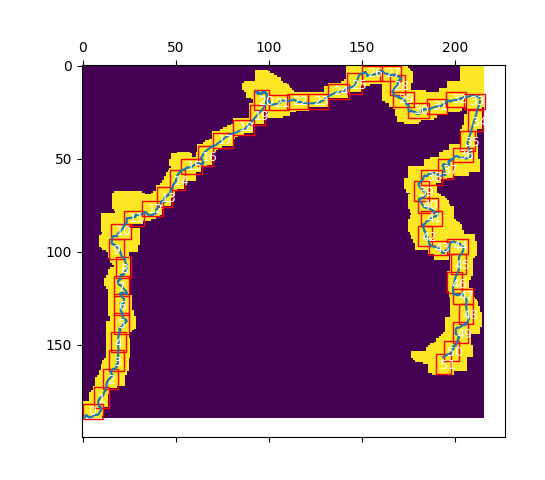
Adding GPX track to charts
I have the means to generate the maps at this point, but still I would like to see where I am going, so I want to add GPX track to my charts. That didn’t sound difficult at first. I just added a cut_path() method to the Box class that loops over GPX coordinates and returns only those points within the Box boundaries. I next used PIL’s line drawing functions to draw a black line from the selected points over the stitched image, before saving it.
draw = ImageDraw.Draw(img)
draw.line(cut_track, fill=(0, 0, 0), width=2)
del draw
This simple approach just had one drawback. It cut the intersections of the track with tile borders. Maybe a small nuisance, but it made me spend some time trying to fix it. I ended up calculating the intersecting points algebraically and then adding them to the begginging and the end at the border of the box.
I had a line section from two points that intersected box’s border. I decided to calculate intersecting points bye simply solving the 2 equation system:
$ \begin{cases} A_1x + B_1y = C_1 \\ A_2x + B_2y = C_2 \end{cases} $
Where $A_1$, $B_1$ and $C_1$ are $Ax + By = C$ line equation coefficients for the line segment and $A_2$, $B_2$ and $C_2$ are the coefficients for the box border.
To obtain the line segment equation coefficients I had to solve the following equation:
$ \begin{cases} Ax_1 + By_1 = C \\ Ax_2 + By_2 = C \end{cases} $
With $x_1$, $y_1$ being coordinates of the first point, and $x_2$ and $y_2$ being coordinates of the second. After some derivation and assuming $C = x_1y_2 - y_1x_2$ I came up with:
$\begin{array} {lcl} A & = & y_2 - y_1 = \Delta y \\ -B & = & x_2 - x_1 = \Delta x \\ C & = & x_1y_2 - y_1x_2 \end{array}$
I’ve made it into a simple function in the utils.py file. I also added a small procedure to compute the point where two lines intersect using Cramer’s rule:
def line(p1, p2):
# Generate line equation Ax + By = C from two given points
return {
'a': p2[1] - p1[1],
'b': p1[0] - p2[0],
'c': p1[0] * p2[1] - p1[1] * p2[0]
}
def line_intersection(l1, l2):
# Return line intersection coordinates,
# None in case lines do not intersect
# I use Cramer's rule tp calculate the intersection
det = l1['a'] * l2['b'] - l1['b'] * l2['a']
if abs(det) < 1e-10:
# Lines parallel
return None
x0 = (l1['c'] * l2['b'] - l1['b'] * l2['c']) / det
y0 = (l1['a'] * l2['c'] - l1['c'] * l2['a']) / det
return (x0, y0)
All of these I added as the add_intersection() function inside Box.cut_path() method. At first I create line coefficients based on the current point and previous point when cutting the track segment. I then create line equations for the top, bottom, left and right borders of the box. In the next step I loop over each border and calculate the intersection with my track segment. Every pair of non-parallel lines will intersect at some point. To select that the intersection is with the border that I am looking for, I check if the intersection is withing a bounding box created by the two points of the segment. If that is the case, I add the intersecting point to the cutted track.
def add_intersection():
""" Add intersection with the Box border for begining or end."""
# Generate line equations Ax + By = C from two points and edges
line = utils.line(prev_pt, pt)
top = {'a': 0, 'b': 1, 'c': self.y1}
bottom = {'a': 0, 'b': 1, 'c': self.y}
left = {'a': 1, 'b': 0, 'c': self.x}
right = {'a': 1, 'b': 0, 'c': self.x1}
# Check intersection of segment with edges
pt_begin = None
for edge in [top, bottom, left, right]:
intersection = utils.line_intersection(line, edge)
if intersection is None:
continue
if self._is_in_range(intersection, pt, prev_pt):
pt_begin = intersection
if pt_begin is not None:
result.append(((pt_begin[0] - self.x) * px_size[0], (pt_begin[1] - self.y) * px_size[1]))
Preparing charts for print
Before printing I also wanted to add a scale to my charts. I added Box.add_scale(self, img, tiles, pos=(0.03, 0.97)) method. It operates on a PIL image and adds a scale for 1km, 5km and 10km at the pos. The scale is calculated using OSM equations. I then add lines and text using PIL.
def add_scale(self, img, tiles, pos=(0.03, 0.97)):
""" Add distance scale to image. """
px_size = tiles.tile_px
x = pos[0] * self.dx * px_size[0]
y = pos[1] * self.dy * px_size[1]
# Get lat for px y coordinate
# From: https://wiki.openstreetmap.org/wiki/Slippy_map_tilenames#Tile_numbers_to_lon..2Flat._2
n = 2.0 ** tiles.zoom
lat_rad = math.atan(math.sinh(math.pi * (1 - 2 * (tiles.tile_range['y'][0] + self.y + pos[1] * self.dy) / n)))
# Get m / px
# https://wiki.openstreetmap.org/wiki/Zoom_levels
C = 2 * math.pi * 6378137.0
m_per_px = C * math.cos(lat_rad) / 2 ** (tiles.zoom + math.log2(px_size[0]))
km1 = 1000 / m_per_px
km5 = 5000 / m_per_px
km10 = 10000 / m_per_px
# Draw lines
draw = ImageDraw.Draw(img)
# Horizontal 10 km line
draw.line((x, y) + (x + km10, y), fill=(0, 0, 0), width=2)
# Add ticks
draw.line((x + km5, y) + (x + km5, y-5), fill=(0, 0, 0), width=2)
draw.line((x + km1, y-5) + (x + km1, y+5), fill=(0, 0, 0), width=2)
draw.line((x, y-7) + (x, y+7), fill=(0, 0, 0), width=2)
# Add annotations
font = ImageFont.truetype("DejaVuSans.ttf", 12)
draw.text(((x, y + 10) ), "0 km", (0, 0, 0), font=font)
draw.text(((x + km1, y + 10) ), "1 km", (0, 0, 0), font=font)
draw.text(((x + km5, y + 10) ), "5 km", (0, 0, 0), font=font)
draw.text(((x + km10, y + 10) ), "10 km", (0, 0, 0), font=font)
del draw
By default I wanted to print the charts using only black and white. For that I added options to change the color of water and add increase contrast before converting it to grayscale image. I first unpack the image into separate R G B channels. I then identify which pixels have RGB values as defined in the water variable. After that I change those pixels in data to white.
data = np.array(img)
# "data" is a height x width x 3 numpy array
red, green, blue = data.T
# Replace colors
water_px = (red == water[0]) & (green == water[1]) & (blue == water[2])
data[:, :][water_px.T] = (255, 255, 255)
img = Image.fromarray(data)
After that I have added the possibility to convert the whole image to grayscale after enhancing contrast:
enhancer = ImageEnhance.Contrast(img)
img = enhancer.enhance(1.25).convert('L')
All these procedures are part of Tiles.generate_maps(self, rectangles, path, track=None, prefix='stitch', water=[None, None, None], gray=False) method.
it takes as arguments list of Boxes, path where to save created images, optional GPX track, prefix under which save the images, optional water RGB values and option to save grayscale images. Sample output can be seen
After creating separate images I went to my local print shop and I got informed that they could not print double sided separate images. They would have to do this manually and with 42 images (10 charts had only water on them) that would take long. So I quickly wrote a script (merge_png.pdf) where PIL loads each image, checks width and height and rotates to portrait if width is greater than height. It also adds the images into TIFF or PDF file. With that I could finally have my maps printed as double sided A3 images.
Downloading missing tiles
At this stage I wanted to have my maps look pretty, but I still had many missing tiles in corners of my maps. So I created a simple TileSource class that allows simple tile downloading. It is created when a URL is provided. It can be passed as an option during Tiles object initialization. It then is used during tile stitching, when the missing tiles are added. This class uses a simple requests query. To not overload the server I added a simple 0.5 s delay after each request. Like the comments say, the code is only preliminary, so it includes only a single download thread and if the connection times out after 10 s it throws an error. I would like to see this improved in the future.
class TileSource:
def __init__(self, source='', destination='', overwrite=False, ask='yes'):
self.source = source
self.destination = destination
self.ask = ask
self.overwrite = overwrite
def download_tiles(self, tiles, zoom):
for idx, tile in enumerate(tiles):
file_exists = os.path.isfile(os.path.join(self.destination, str(zoom), str(tile[0]), str(tile[1]) + '.png'))
if file_exists and not self.overwrite:
continue
print('\r', 'Downloading {}/{}'.format(idx+1, len(tiles)), end='')
self._get_tile(tile, zoom)
# TODO: Better sleep + threads + error handeling
time.sleep(0.5)
print()
def _get_tile(self, tile, zoom):
url = self.source.format(**{'z': zoom, 'x': tile[0], 'y': tile[1]})
r = requests.get(url, timeout=10)
if r.status_code == 200:
path = os.path.join(self.destination, str(zoom), str(tile[0]))
if not os.path.exists(path):
os.makedirs(path)
with open(os.path.join(path, str(tile[1]) + '.png'), 'wb') as f:
f.write(r.content)
else:
print("Download error for: %s\n%s" % (r.url, r))
Programme usage
Finally I packed everything into a neat Python command. All the code is avaliable here.
I wrote it under Python 3.7. I used the following dependencies: requests, Numpy, Matplotlib, Pillow and gpxpy.
All the modules should be available through pip.
The script allows to either work with tiles offline or to speciffy a tile server URL in the --dl option. The script will then create subdirectories for the zoom levels and download tiles. I tested this option using OpenCycleMap after registering and obtaining the API key. I find it somehow much better for printing than OSM tiles.
NOTE: Before usage the script needs to have the tiles and output directories already present. The script overwrites output maps, so please work in different directories when working with different tiles.
Usage:
usage: print.py [-h] [-z ZOOM] --gpx GPX [-o OUTPUT_DIR] [-p MAP_PREFIX]
[--gray] [--water WATER WATER WATER] [-x NX] [-y NY]
[--dl TILE_DL]
tile_path
positional arguments:
tile_pathDirectory with OSM PNG tiles: ./{zoom}/{x}/{y}.png
optional arguments:
-h, --helpshow this help message and exit-z ZOOMOSM zoom level--gpx GPXGPX trace to produce maps-o OUTPUT_DIRoutput maps directory-p MAP_PREFIXoutput map prefix, ‘stitch’ by default--grayoutput as grayscale--water R G Bremoves water color given as R G B byte values; e.g.--water 170 211 223for OSM-x NXnumber of tiles in X dimension to load per chart; 8 by default-y NYnumber of tiles in Y dimension to load per chart; 11 by default--dl TILE_DLURL for downloading missing tiles, e.g.:--dl https://a.tile.openstreetmap.org/{z}/{x}/{y}.pngfor OSM
An example using OpenCycleMap tiles:
python print.py ./tiles/bike -z 13 --gray --gpx ./routes/cycle_travel2.gpx -o \
./map/bike --water 173 222 255 --dl https://tile.thunderforest.com/cycle/{z}/{x}/{y}.png?apikey=...
Conclusions
In the end it took me couple of days to work this thing out. It is still far from perfect, but it serves its use. I was able to successfully create and print A3 maps for my journey. Now I won’t get lost in case my phone dies or gets wet.
In the end I extremely enjoyed working on this mini-project. I had a great opportunity to learn image manipulation in Python as well as refresh some basic level algebra. What’s more important though is that I was able to overcome doubt whispering that this is not worth my time. I remember being in this flow mode couple of times when working on it. I just hope that I will be able to work on similar practical probelm solving exercises in the future!